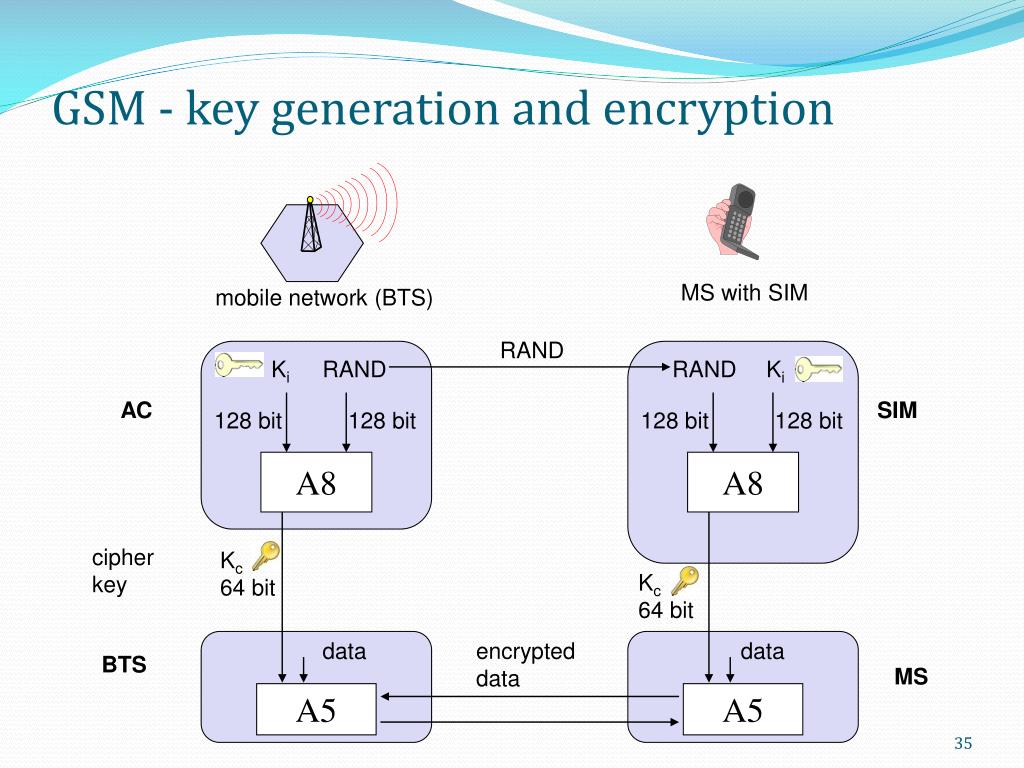
Gsm Key Generation And Encryption Process
A5/1 is a stream cipher used to provide over-the-air communication privacy in the GSMcellular telephone standard. It is one of seven algorithms which were specified for GSM use.[1] It was initially kept secret, but became public knowledge through leaks and reverse engineering. A number of serious weaknesses in the cipher have been identified.
History and usage[edit]
CALL ROUTING IN GSM UNIT - 2 Prepared By:- NITIN PANDYA. A5 algorithm for encryption - A8 algorithm for key generation 21 NITIN PANDYA. Authentication Concept Random Number Generator Authentication. During the authentication process the MSC. We will see two aspects of the RSA cryptosystem, firstly generation of key pair and secondly encryption-decryption algorithms. Generation of RSA Key Pair. Each person or a party who desires to participate in communication using encryption needs to generate a pair of keys, namely public key and private key. The process followed in the generation.
A5/1 is used in Europe and the United States. A5/2 was a deliberate weakening of the algorithm for certain export regions.[2] A5/1 was developed in 1987, when GSM was not yet considered for use outside Europe, and A5/2 was developed in 1989. Though both were initially kept secret, the general design was leaked in 1994 and the algorithms were entirely reverse engineered in 1999 by Marc Briceno from a GSM telephone. In 2000, around 130 million GSM customers relied on A5/1 to protect the confidentiality of their voice communications; by 2014, it was 7.2 billion.[3]
We would capture gsm data in wireshark through osmocom-bb and analyse how the entire process of gsm authentication and encryption happens. We will also see how the location update process happens. In GSM, KASUMI is used in the A5/3 key stream generator and in GPRS in the GEA3 key stream generator. Generation of encryption key(Kc). GSM/GPRS, uses the concept of Authentication Vector (AV) but unlike GSM/GPRS, the AV comprises of five components: the random challenge (RAND), the expected response (XRES), key for encryption (CK), integrity key (IK) and the authentication token (AUTN). The VLR/SGSN requests HLR/AuC for authentication. The Ki – the root encryption key. This is a randomly generated 128-bit number allocated to a particular subscriber that seeds the generation of all keys and challenges used in the GSM system. The Ki is highly protected, and is only known in the SIM and the network’s AuC (Authentication Centre). Usage of OP/OPc and Transport Key OP: Operator Code: It is allotted to an operator and used in key generation algorithms of 3G and 4G. It is not shown as a part of input, because it is not specific to a user/Subscriber/SIM. Then they are provisioned in encrypted form rather then plain and this encryption is done by Transport Key. What is GSM Encryption? GSM is the abbreviated term for General System for Mobile communications and this is known as a standard for the mobile phone telephony system. And, the process in which phone conversations is messed up via a network while making use of GSM is called GSM encryption.
Security researcher Ross Anderson reported in 1994 that 'there was a terrific row between the NATOsignal intelligence agencies in the mid-1980s over whether GSM encryption should be strong or not. The Germans said it should be, as they shared a long border with the Warsaw Pact; but the other countries didn't feel this way, and the algorithm as now fielded is a French design.'[4]
Description[edit]
A GSM transmission is organised as sequences of bursts. In a typical channel and in one direction, one burst is sent every 4.615 milliseconds and contains 114 bits available for information. A5/1 is used to produce for each burst a 114 bit sequence of keystream which is XORed with the 114 bits prior to modulation. A5/1 is initialised using a 64-bit key together with a publicly known 22-bit frame number. Older fielded GSM implementations using Comp128v1 for key generation, had 10 of the key bits fixed at zero, resulting in an effective key length of 54 bits. This weakness was rectified with the introduction of Comp128v3 which yields proper 64 bits keys. When operating in GPRS / EDGE mode, higher bandwidth radio modulation allows for larger 348 bits frames, and A5/3 is then used in a stream cipher mode to maintain confidentiality.
A5/1 is based around a combination of three linear feedback shift registers (LFSRs) with irregular clocking. The three shift registers are specified as follows:
| LFSR number | Length in bits | Feedback polynomial | Clocking bit | Tapped bits |
|---|---|---|---|---|
| 1 | 19 | 8 | 13, 16, 17, 18 | |
| 2 | 22 | 10 | 20, 21 | |
| 3 | 23 | 10 | 7, 20, 21, 22 |
The bits are indexed with the least significant bit (LSB) as 0.
The registers are clocked in a stop/go fashion using a majority rule. Each register has an associated clocking bit. At each cycle, the clocking bit of all three registers is examined and the majority bit is determined. A register is clocked if the clocking bit agrees with the majority bit. Hence at each step at least two or three registers are clocked, and each register steps with probability 3/4.
Initially, the registers are set to zero. Then for 64 cycles, the 64-bit secret key is mixed in according to the following scheme: in cycle , the ith key bit is added to the least significant bit of each register using XOR —
Each register is then clocked.
Similarly, the 22-bits of the frame number are added in 22 cycles. Then the entire system is clocked using the normal majority clocking mechanism for 100 cycles, with the output discarded. After this is completed, the cipher is ready to produce two 114 bit sequences of output keystream, first 114 for downlink, last 114 for uplink.
Security[edit]
A number of attacks on A5/1 have been published, and the American National Security Agency is able to routinely decrypt A5/1 messages according to released internal documents.[5]
Some attacks require an expensive preprocessing stage after which the cipher can be broken in minutes or seconds. Until recently, the weaknesses have been passive attacks using the known plaintext assumption. In 2003, more serious weaknesses were identified which can be exploited in the ciphertext-only scenario, or by an active attacker. In 2006 Elad Barkan, Eli Biham and Nathan Keller demonstrated attacks against A5/1, A5/3, or even GPRS that allow attackers to tap GSM mobile phone conversations and decrypt them either in real-time, or at any later time.
According to professor Jan Arild Audestad, at the standardization process which started in 1982, A5/1 was originally proposed to have a key length of 128 bits. At that time, 128 bits was projected to be secure for at least 15 years. It is now believed that 128 bits would in fact also still be secure until the advent of quantum computing. Audestad, Peter van der Arend, and Thomas Haug says that the British insisted on weaker encryption, with Haug saying he was told by the British delegate that this was to allow the British secret service to eavesdrop more easily. The British proposed a key length of 48 bits, while the West Germans wanted stronger encryption to protect against East German spying, so the compromise became a key length of 54 bits.[6]
Known-plaintext attacks[edit]
The first attack on the A5/1 was proposed by Ross Anderson in 1994. Anderson's basic idea was to guess the complete content of the registers R1 and R2 and about half of the register R3. In this way the clocking of all three registers is determined and the second half of R3 can be computed.[4]
In 1997, Golic presented an attack based on solving sets of linear equations which has a time complexity of 240.16 (the units are in terms of number of solutions of a system of linear equations which are required).
In 2000, Alex Biryukov, Adi Shamir and David Wagner showed that A5/1 can be cryptanalysed in real time using a time-memory tradeoff attack,[7] based on earlier work by Jovan Golic.[8] One tradeoff allows an attacker to reconstruct the key in one second from two minutes of known plaintext or in several minutes from two seconds of known plain text, but he must first complete an expensive preprocessing stage which requires 248 steps to compute around 300 GB of data. Several tradeoffs between preprocessing, data requirements, attack time and memory complexity are possible.
The same year, Eli Biham and Orr Dunkelman also published an attack on A5/1 with a total work complexity of 239.91 A5/1 clockings given 220.8 bits of known plaintext. The attack requires 32 GB of data storage after a precomputation stage of 238.[9]
Ekdahl and Johansson published an attack on the initialisation procedure which breaks A5/1 in a few minutes using two to five minutes of conversation plaintext.[10] This attack does not require a preprocessing stage. In 2004, Maximov et al. improved this result to an attack requiring 'less than one minute of computations, and a few seconds of known conversation'. The attack was further improved by Elad Barkan and Eli Biham in 2005.[11]
Attacks on A5/1 as used in GSM[edit]
In 2003, Barkan et al. published several attacks on GSM encryption.[12] The first is an active attack. GSM phones can be convinced to use the much weaker A5/2 cipher briefly. A5/2 can be broken easily, and the phone uses the same key as for the stronger A5/1 algorithm. A second attack on A5/1 is outlined, a ciphertext-only time-memory tradeoff attack which requires a large amount of precomputation.
In 2006, Elad Barkan, Eli Biham, Nathan Keller published the full version of their 2003 paper, with attacks against A5/X сiphers. The authors claim:[13]
We present a very practical ciphertext-only cryptanalysis of GSM encrypted communication, and various active attacks on the GSM protocols. These attacks can even break into GSM networks that use 'unbreakable' ciphers. We first describe a ciphertext-only attack on A5/2 that requires a few dozen milliseconds of encrypted off-the-air cellular conversation and finds the correct key in less than a second on a personal computer. We extend this attack to a (more complex) ciphertext-only attack on A5/1. We then describe new (active) attacks on the protocols of networks that use A5/1, A5/3, or even GPRS. These attacks exploit flaws in the GSM protocols, and they work whenever the mobile phone supports a weak cipher such as A5/2. We emphasize that these attacks are on the protocols, and are thus applicable whenever the cellular phone supports a weak cipher, for example, they are also applicable for attacking A5/3 networks using the cryptanalysis of A5/1. Unlike previous attacks on GSM that require unrealistic information, like long known plaintext periods, our attacks are very practical and do not require any knowledge of the content of the conversation. Furthermore, we describe how to fortify the attacks to withstand reception errors. As a result, our attacks allow attackers to tap conversations and decrypt them either in real-time, or at any later time.
In 2007 Universities of Bochum and Kiel started a research project to create a massively parallel FPGA-based cryptographic accelerator COPACOBANA. COPACOBANA was the first commercially available solution[14] using fast time-memory trade-off techniques that could be used to attack the popular A5/1 and A5/2 algorithms, used in GSM voice encryption, as well as the Data Encryption Standard (DES). It also enables brute force attacks against GSM eliminating the need of large precomputed lookup tables.
In 2008, the group The Hackers Choice launched a project to develop a practical attack on A5/1. The attack requires the construction of a large look-up table of approximately 3 terabytes. Together with the scanning capabilities developed as part of the sister project, the group expected to be able to record any GSM call or SMS encrypted with A5/1, and within about 3–5 minutes derive the encryption key and hence listen to the call and read the SMS in clear. But the tables weren't released.[15]
A similar effort, the A5/1 Cracking Project, was announced at the 2009 Black Hat security conference by cryptographers Karsten Nohl and Sascha Krißler. It created the look-up tables using NvidiaGPGPUs via a peer-to-peerdistributed computing architecture. Starting in the middle of September 2009, the project ran the equivalent of 12 Nvidia GeForce GTX 260. According to the authors, the approach can be used on any cipher with key size up to 64-bits.[16]
In December 2009, the A5/1 Cracking Project attack tables for A5/1 were announced by Chris Paget and Karsten Nohl. The tables use a combination of compression techniques, including rainbow tables and distinguished point chains. These tables constituted only parts of the 1.7 TB completed table and had been computed during three months using 40 distributed CUDA nodes and then published over BitTorrent and Google drive that is provided by community member Farid Nasiri [15][16][17][18][19] More recently the project has announced a switch to faster ATI Evergreen code, together with a change in the format of the tables and Frank A. Stevenson announced breaks of A5/1 using the ATI generated tables.[20]
Documents leaked by Edward Snowden in 2013 state that the NSA 'can process encrypted A5/1'.[21]
See also[edit]
- KASUMI, also known as A5/3
Notes[edit]
- ^'Prohibiting A5/2 in mobile stations and other clarifications regarding A5 algorithm support'.
- ^Quirke, Jeremy (1 May 2004). 'Security in the GSM system'(PDF). AusMobile. Archived from the original(PDF) on 12 July 2004. Retrieved 8 September 2008.
- ^'There are officially more mobile devices than people in the world'. The Independent. 7 October 2014. Retrieved 19 December 2017.
- ^ abRoss Anderson (17 June 1994). 'A5 (Was: HACKING DIGITAL PHONES)'. Newsgroup: uk.telecom. Usenet:2ts9a0$95r@lyra.csx.cam.ac.uk.
- ^NSA Able To Crack A5/1 Cellphone Crypto - Slashdot
- ^http://www.aftenposten.no/nyheter/uriks/Sources-We-were-pressured-to-weaken-the-mobile-security-in-the-80s-7413285.html#.UtBeNpD_sQs
- ^Biryukov, Alex; Adi Shamir; David Wagner. 'Real Time Cryptanalysis of A5/1 on a PC'. Fast Software Encryption—FSE 2000: 1–18.
- ^Golic, Jovan Dj. (1997). 'Cryptanalysis of Alleged A5 Stream Cipher'(PDF). Eurocrypt 1997: 239–55. Archived from the original(PDF) on 15 July 2010. Retrieved 13 January 2016.
- ^Biham, Eli; Orr Dunkelman (2000). 'Cryptanalysis of the A5/1 GSM Stream Cipher'. Indocrypt 2000. Lecture Notes in Computer Science. 1977: 43–51. doi:10.1007/3-540-44495-5_5. ISBN978-3-540-41452-0.
- ^Ekdahl, Patrik; Thomas Johansson (2003). 'Another attack on A5/1'(PDF). IEEE Transactions on Information Theory. 49 (1): 284–89. doi:10.1109/TIT.2002.806129. Archived from the original(PDF) on 25 May 2005.
- ^Barkan, Elad; Eli Biham (2005). 'Conditional Estimators: An Effective Attack on A5/1'. Selected Areas in Cryptography 2005: 1–19.
- ^Barkan, Elad; Eli Biham; Nathan Keller (2003). 'Instant Ciphertext-Only Cryptanalysis of GSM Encrypted Communication'(PDF). Crypto 2003. Lecture Notes in Computer Science. 2729: 600–16. doi:10.1007/978-3-540-45146-4_35. ISBN978-3-540-40674-7.
- ^Barkan, Elad; Eli Biham; Nathan Keller. 'Instant Ciphertext-Only Cryptanalysis of GSM Encrypted Communication by Barkan and Biham of Technion (Full Version)'(PDF).
- ^Gueneysu, Tim; Timo Kasper; Martin Novotný; Christof Paar; Andy Rupp (2008). 'Cryptanalysis with COPACOBANA'(PDF). IEEE Transactions on Computers. 57 (11): 1498–1513. doi:10.1109/TC.2008.80.
- ^ abNohl, Karsten; Chris Paget (27 December 2009). GSM: SRSLY?. 26th Chaos Communication Congress (26C3). Archived from the original on 6 January 2010. Retrieved 30 December 2009.
- ^ ab'Archived copy'(PDF). Archived from the original(PDF) on 26 July 2011. Retrieved 29 December 2009.CS1 maint: archived copy as title (link) Subverting the security base of GSM. Karsten Nohl and Sascha Krißler
- ^O'Brien, Kevin (28 December 2009). 'Cellphone Encryption Code Is Divulged'. New York Times. Archived from the original on 29 April 2011. Retrieved 29 December 2009.
- ^McMillan, Robert. 'Hackers Show It's Easy to Snoop on a GSM Call'. IDG News Service.
- ^Nohl, Karsten. 'Direct Link A5/1 rainbow Table in Google drive'.
- ^Frank A. Stevenson (1 May 2010). 'Cracks beginning to show in A5/1'. Archived from the original on 6 March 2012.
- ^Timberg, Craig; Soltani, Ashkan (13 December 2013). 'By cracking cellphone code, NSA has ability to decode private conversations'. The Washington Post. Retrieved 28 September 2016.
References[edit]
- Rose, Greg (10 September 2003). 'A precis of the new attacks on GSM encryption'(PDF). QUALCOMM Australia.
- Maximov, Alexander; Thomas Johansson; Steve Babbage (2004). 'An Improved Correlation Attack on A5/1'. Selected Areas in Cryptography 2004: 1–18.
External links[edit]
- Briceno, Marc; Ian Goldberg; David Wagner (23 October 1999). 'A pedagogical implementation of the GSM A5/1 and A5/2 'voice privacy' encryption algorithms'.
- 'Huge GSM flaw allows hackers to listen in on voice calls'. 25 August 2009. Archived from the original on 14 October 2009.
- Horesh, Hadar (3 September 2003). 'Technion team cracks GSM cellular phone encryption'(PDF). Haaretz.
- Barkan, Elad; Eli Biham; Nathan Keller (July 2006). 'Instant Ciphertext-Only Cryptanalysis of GSM Encrypted Communication (Technical Report CS-2006-07)'.
- 'Nathan Keller's Homepage'. Archived from the original on 4 June 2008.
- 'Animated SVG showing A5/1 stream cypher'. Archived from the original on 26 March 2012.
- Cryptography Tutorial
- Cryptography Useful Resources
- Selected Reading
Public Key Cryptography
Unlike symmetric key cryptography, we do not find historical use of public-key cryptography. It is a relatively new concept.
Symmetric cryptography was well suited for organizations such as governments, military, and big financial corporations were involved in the classified communication.
With the spread of more unsecure computer networks in last few decades, a genuine need was felt to use cryptography at larger scale. The symmetric key was found to be non-practical due to challenges it faced for key management. This gave rise to the public key cryptosystems.
The process of encryption and decryption is depicted in the following illustration −
The most important properties of public key encryption scheme are −
Different keys are used for encryption and decryption. This is a property which set this scheme different than symmetric encryption scheme.
Each receiver possesses a unique decryption key, generally referred to as his private key.
Receiver needs to publish an encryption key, referred to as his public key.
Some assurance of the authenticity of a public key is needed in this scheme to avoid spoofing by adversary as the receiver. Generally, this type of cryptosystem involves trusted third party which certifies that a particular public key belongs to a specific person or entity only.
Encryption algorithm is complex enough to prohibit attacker from deducing the plaintext from the ciphertext and the encryption (public) key.
Though private and public keys are related mathematically, it is not be feasible to calculate the private key from the public key. In fact, intelligent part of any public-key cryptosystem is in designing a relationship between two keys.
There are three types of Public Key Encryption schemes. We discuss them in following sections −
RSA Cryptosystem
This cryptosystem is one the initial system. It remains most employed cryptosystem even today. The system was invented by three scholars Ron Rivest, Adi Shamir, and Len Adleman and hence, it is termed as RSA cryptosystem.
We will see two aspects of the RSA cryptosystem, firstly generation of key pair and secondly encryption-decryption algorithms.
Generation of RSA Key Pair
Each person or a party who desires to participate in communication using encryption needs to generate a pair of keys, namely public key and private key. The process followed in the generation of keys is described below −
Generate the RSA modulus (n)
Select two large primes, p and q.
Calculate n=p*q. For strong unbreakable encryption, let n be a large number, typically a minimum of 512 bits.
Find Derived Number (e)
Number e must be greater than 1 and less than (p − 1)(q − 1).
There must be no common factor for e and (p − 1)(q − 1) except for 1. In other words two numbers e and (p – 1)(q – 1) are coprime.
Form the public key
The pair of numbers (n, e) form the RSA public key and is made public.
Interestingly, though n is part of the public key, difficulty in factorizing a large prime number ensures that attacker cannot find in finite time the two primes (p & q) used to obtain n. This is strength of RSA.
Generate the private key
Private Key d is calculated from p, q, and e. For given n and e, there is unique number d.
Number d is the inverse of e modulo (p - 1)(q – 1). This means that d is the number less than (p - 1)(q - 1) such that when multiplied by e, it is equal to 1 modulo (p - 1)(q - 1).
This relationship is written mathematically as follows −
The Extended Euclidean Algorithm takes p, q, and e as input and gives d as output.
Example
An example of generating RSA Key pair is given below. (For ease of understanding, the primes p & q taken here are small values. Practically, these values are very high).
Let two primes be p = 7 and q = 13. Thus, modulus n = pq = 7 x 13 = 91.
Select e = 5, which is a valid choice since there is no number that is common factor of 5 and (p − 1)(q − 1) = 6 × 12 = 72, except for 1.
The pair of numbers (n, e) = (91, 5) forms the public key and can be made available to anyone whom we wish to be able to send us encrypted messages.
Input p = 7, q = 13, and e = 5 to the Extended Euclidean Algorithm. The output will be d = 29.
Check that the d calculated is correct by computing −
Hence, public key is (91, 5) and private keys is (91, 29).
Encryption and Decryption
Once the key pair has been generated, the process of encryption and decryption are relatively straightforward and computationally easy.
Interestingly, RSA does not directly operate on strings of bits as in case of symmetric key encryption. It operates on numbers modulo n. Hence, it is necessary to represent the plaintext as a series of numbers less than n.
RSA Encryption
Suppose the sender wish to send some text message to someone whose public key is (n, e).
The sender then represents the plaintext as a series of numbers less than n.
To encrypt the first plaintext P, which is a number modulo n. The encryption process is simple mathematical step as −
In other words, the ciphertext C is equal to the plaintext P multiplied by itself e times and then reduced modulo n. This means that C is also a number less than n.
Returning to our Key Generation example with plaintext P = 10, we get ciphertext C −
RSA Decryption
The decryption process for RSA is also very straightforward. Suppose that the receiver of public-key pair (n, e) has received a ciphertext C.
Receiver raises C to the power of his private key d. The result modulo n will be the plaintext P.
Returning again to our numerical example, the ciphertext C = 82 would get decrypted to number 10 using private key 29 −
RSA Analysis
The security of RSA depends on the strengths of two separate functions. The RSA cryptosystem is most popular public-key cryptosystem strength of which is based on the practical difficulty of factoring the very large numbers.
Encryption Function − It is considered as a one-way function of converting plaintext into ciphertext and it can be reversed only with the knowledge of private key d.
Key Generation − The difficulty of determining a private key from an RSA public key is equivalent to factoring the modulus n. An attacker thus cannot use knowledge of an RSA public key to determine an RSA private key unless he can factor n. It is also a one way function, going from p & q values to modulus n is easy but reverse is not possible.
If either of these two functions are proved non one-way, then RSA will be broken. In fact, if a technique for factoring efficiently is developed then RSA will no longer be safe.
The strength of RSA encryption drastically goes down against attacks if the number p and q are not large primes and/ or chosen public key e is a small number.
ElGamal Cryptosystem
Along with RSA, there are other public-key cryptosystems proposed. Many of them are based on different versions of the Discrete Logarithm Problem.
ElGamal cryptosystem, called Elliptic Curve Variant, is based on the Discrete Logarithm Problem. It derives the strength from the assumption that the discrete logarithms cannot be found in practical time frame for a given number, while the inverse operation of the power can be computed efficiently.

Let us go through a simple version of ElGamal that works with numbers modulo p. In the case of elliptic curve variants, it is based on quite different number systems.
Generation of ElGamal Key Pair
Each user of ElGamal cryptosystem generates the key pair through as follows −
Choosing a large prime p. Generally a prime number of 1024 to 2048 bits length is chosen.
Choosing a generator element g.
This number must be between 1 and p − 1, but cannot be any number.
It is a generator of the multiplicative group of integers modulo p. This means for every integer m co-prime to p, there is an integer k such that gk=a mod n.
For example, 3 is generator of group 5 (Z5 = {1, 2, 3, 4}).
| N | 3n | 3n mod 5 |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 9 | 4 |
| 3 | 27 | 2 |
| 4 | 81 | 1 |
Choosing the private key. The private key x is any number bigger than 1 and smaller than p−1.
Computing part of the public key. The value y is computed from the parameters p, g and the private key x as follows −
Obtaining Public key. The ElGamal public key consists of the three parameters (p, g, y).
For example, suppose that p = 17 and that g = 6 (It can be confirmed that 6 is a generator of group Z17). The private key x can be any number bigger than 1 and smaller than 71, so we choose x = 5. The value y is then computed as follows −
Thus the private key is 62 and the public key is (17, 6, 7).
Encryption and Decryption
The generation of an ElGamal key pair is comparatively simpler than the equivalent process for RSA. But the encryption and decryption are slightly more complex than RSA.
ElGamal Encryption
Suppose sender wishes to send a plaintext to someone whose ElGamal public key is (p, g, y), then −
Sender represents the plaintext as a series of numbers modulo p.
To encrypt the first plaintext P, which is represented as a number modulo p. The encryption process to obtain the ciphertext C is as follows −
- Randomly generate a number k;
- Compute two values C1 and C2, where −
Send the ciphertext C, consisting of the two separate values (C1, C2), sent together.
Referring to our ElGamal key generation example given above, the plaintext P = 13 is encrypted as follows −
- Randomly generate a number, say k = 10
- Compute the two values C1 and C2, where −
Send the ciphertext C = (C1, C2) = (15, 9).
ElGamal Decryption
To decrypt the ciphertext (C1, C2) using private key x, the following two steps are taken −
Compute the modular inverse of (C1)x modulo p, which is (C1)-x , generally referred to as decryption factor.
Obtain the plaintext by using the following formula −
In our example, to decrypt the ciphertext C = (C1, C2) = (15, 9) using private key x = 5, the decryption factor is
Extract plaintext P = (9 × 9) mod 17 = 13.
ElGamal Analysis
In ElGamal system, each user has a private key x. and has three components of public key − prime modulus p, generator g, and public Y = gx mod p. The strength of the ElGamal is based on the difficulty of discrete logarithm problem.
The secure key size is generally > 1024 bits. Today even 2048 bits long key are used. On the processing speed front, Elgamal is quite slow, it is used mainly for key authentication protocols. Due to higher processing efficiency, Elliptic Curve variants of ElGamal are becoming increasingly popular.
Elliptic Curve Cryptography (ECC)
Gsm Key Generation And Encryption Processor
Elliptic Curve Cryptography (ECC) is a term used to describe a suite of cryptographic tools and protocols whose security is based on special versions of the discrete logarithm problem. It does not use numbers modulo p.
ECC is based on sets of numbers that are associated with mathematical objects called elliptic curves. There are rules for adding and computing multiples of these numbers, just as there are for numbers modulo p.
ECC includes a variants of many cryptographic schemes that were initially designed for modular numbers such as ElGamal encryption and Digital Signature Algorithm.
It is believed that the discrete logarithm problem is much harder when applied to points on an elliptic curve. This prompts switching from numbers modulo p to points on an elliptic curve. Also an equivalent security level can be obtained with shorter keys if we use elliptic curve-based variants.
The shorter keys result in two benefits −
- Ease of key management
- Efficient computation
These benefits make elliptic-curve-based variants of encryption scheme highly attractive for application where computing resources are constrained.
RSA and ElGamal Schemes – A Comparison
Let us briefly compare the RSA and ElGamal schemes on the various aspects.
Gsm Key Generation And Encryption Process 2
| RSA | ElGamal |
|---|---|
| It is more efficient for encryption. | It is more efficient for decryption. |
| It is less efficient for decryption. | It is more efficient for decryption. |
| For a particular security level, lengthy keys are required in RSA. | For the same level of security, very short keys are required. |
| It is widely accepted and used. | It is new and not very popular in market. |